作者：韩信子 @ShowMeAI
教程地址 ：http://www.showmeai.tech/tutorials/35
本文地址 ：http://www.showmeai.tech/article-detail/217
声明：版权所有，转载请联系平台与作者并注明出处
收藏ShowMeAI 查看更多精彩内容

---

本系列为吴恩达老师《深度学习专项课程 (Deep Learning Specialization) 》学习与总结整理所得，对应的课程视频可以在 这里 查看。

---

在ShowMeAI 前一篇文章 深度学习的实用层面 中我们对以下内容进行了介绍：

• Train / Dev / Test sets 的切分和比例选择
• Bias 和 Variance 的相关知识
• 防止过拟合的方法：L2 正则化和 Dropout
• 规范化输入以加快梯度下降速度和精度
• 梯度消失和梯度爆炸的原因及处理方法
• 梯度检查

本篇内容展开介绍深度神经网络中的一些优化算法，通过使用这些技巧和方法来提高神经网络的训练速度和精度。

Batch梯度下降法 (批梯度下降法) 是最常用的梯度下降形式，它是基于整个训练集的梯度下降算法，在更新参数时使用所有的样本来进行更新。

对整个训练集进行梯度下降法的时候，我们必须处理整个训练数据集，然后才能进行一步梯度下降，即每一步梯度下降法需要对整个训练集进行一次处理，如果训练数据集很大的时候，处理速度就会比较慢。

但是如果每次处理训练数据的一部分，基于这个子集进行梯度下降法，算法迭代速度会更快。而处理的这些一小部分训练子集即称为 Mini-Batch，这个算法也就是我们说的 Mini-Batch 梯度下降法。

Mini-Batch梯度下降法 (小批量梯度下降法) 每次同时处理单个的 Mini-Batch，其他与 Batch 梯度下降法一致。

使用 Batch 梯度下降法，对整个训练集的一次遍历只能做一个梯度下降；而使用 Mini-Batch 梯度下降法，对整个训练集的一次遍历 (称为一个 epoch) 能做 Mini-Batch 个数个梯度下降。之后，可以一直遍历训练集，直到最后收敛到一个合适的精度。

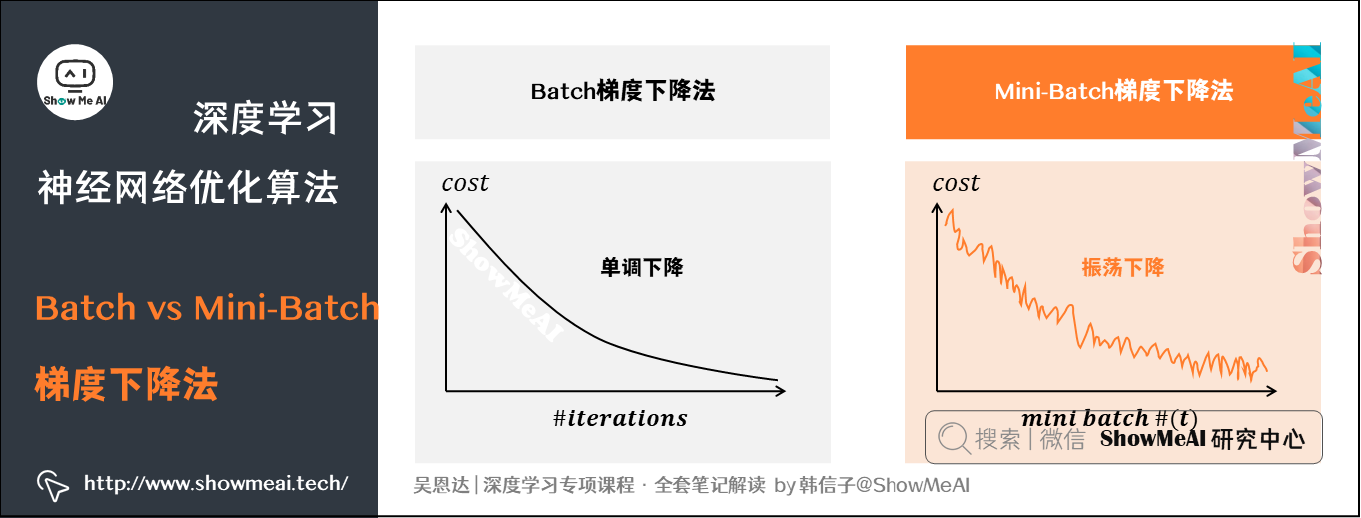
Batch 梯度下降法和 Mini-Batch 梯度下降法代价函数的变化趋势如上图所示：

• 使用 Batch gradient descent，随着迭代次数增加，cost 是不断减小的。
• 使用 Mini-batch gradient descent，随着在不同的 mini-batch 上迭代训练，cost 并不是单调下降，而是振荡下降的，最终也能得到较低的 cost 值。出现细微振荡的原因是不同的 mini-batch 之间是有差异的。例如可能第一个子集 是好的子集，而第二个子集 包含了一些噪声noise。出现细微振荡是正常的。

我们在训练神经网络的时候，使用mini-batch gradient descent，经常要指定一个batch批次的样本数量。而不同的batch大小会影响训练的过程，其中有2个特例，mini-batch gradient descent会退化为不同的算法：

• Mini-Batch的大小为1，即是随机梯度下降法 (stochastic gradient descent) ，每个样本都是独立的 Mini-Batch。
• Mini-Batch的大小为 (数据集大小) ，即是 Batch 梯度下降法。

如上图，我们对比一下Batch gradient descent和Stachastic gradient descent的梯度下降曲线。

• 图中蓝色的线代表Batch gradient descent。Batch gradient descent会比较平稳地接近全局最小值，但是因为使用了所有m个样本，每次前进的速度有些慢。
• 图中紫色的线代表Stochastic gradient descent。Stochastic gradient descent每次前进速度很快，但是路线曲折，有较大的振荡，最终会在最小值附近来回波动，难以真正达到最小值处。而且在数值处理上就不能使用向量化的方法来提高运算速度。

• 对所有 m 个训练样本执行一次梯度下降，每一次迭代时间较长，训练过程慢。
• 相对噪声低一些，幅度也大一些。
• 成本函数总是向减小的方向下降。

• 对每一个训练样本执行一次梯度下降，训练速度快，但丢失了向量化带来的计算加速。
• 有很多噪声，减小学习率可以适当。
• 成本函数总体趋势向全局最小值靠近，但永远不会收敛，而是一直在最小值附近波动。

实际使用中，batch size 不能设置得太大 (会倾向于Batch gradient descent) ，也不能设置得太小 (倾向于Stochastic gradient descent)。

选择一个【1<size<m】的合适的大小进行 Mini-Batch 梯度下降，可以实现快速学习，也应用了向量化带来的好处，且成本函数的下降处于前两者之间。

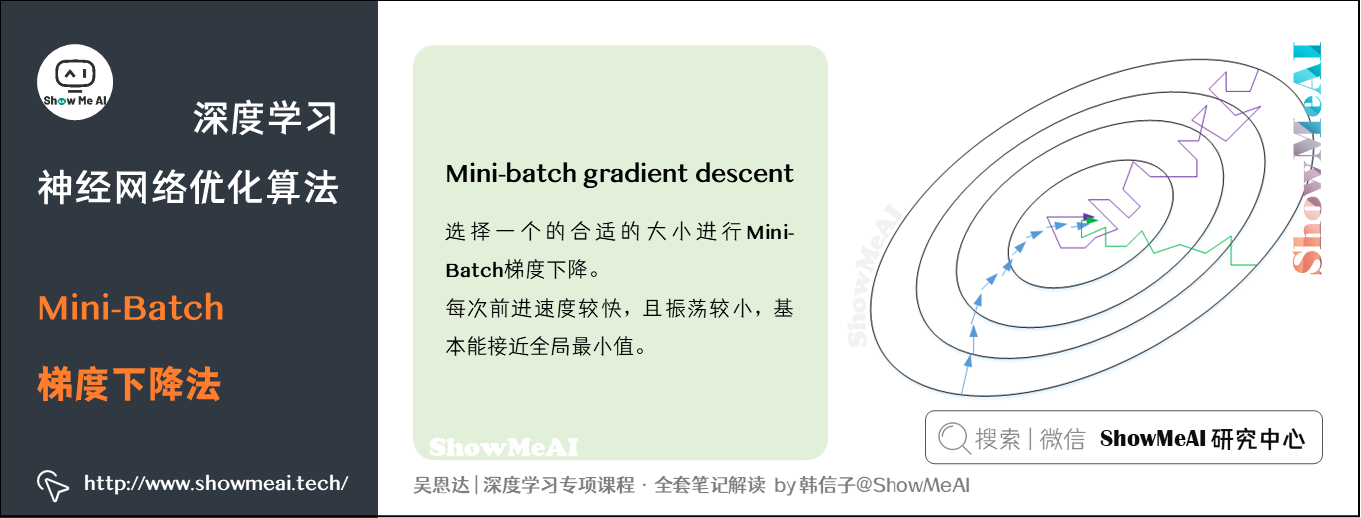
mini-batch gradient descent 的梯度下降曲线如图绿色曲线所示，每次前进速度较快，且振荡较小，基本能接近全局最小值。

吴恩达老师也给出了一些关于 batch 大小选择的经验：

• 训练样本量小 (如 ) ，选择Batch梯度下降法。
• 训练样本量大，选择 Mini-Batch 梯度下降法。
• 与计算机的信息存储方式相适应，代码在Batch大小为2的幂次时运行要快一些，典型的大小为 、、…、 。
• Batch 的大小要匹配 CPU/GPU 内存。

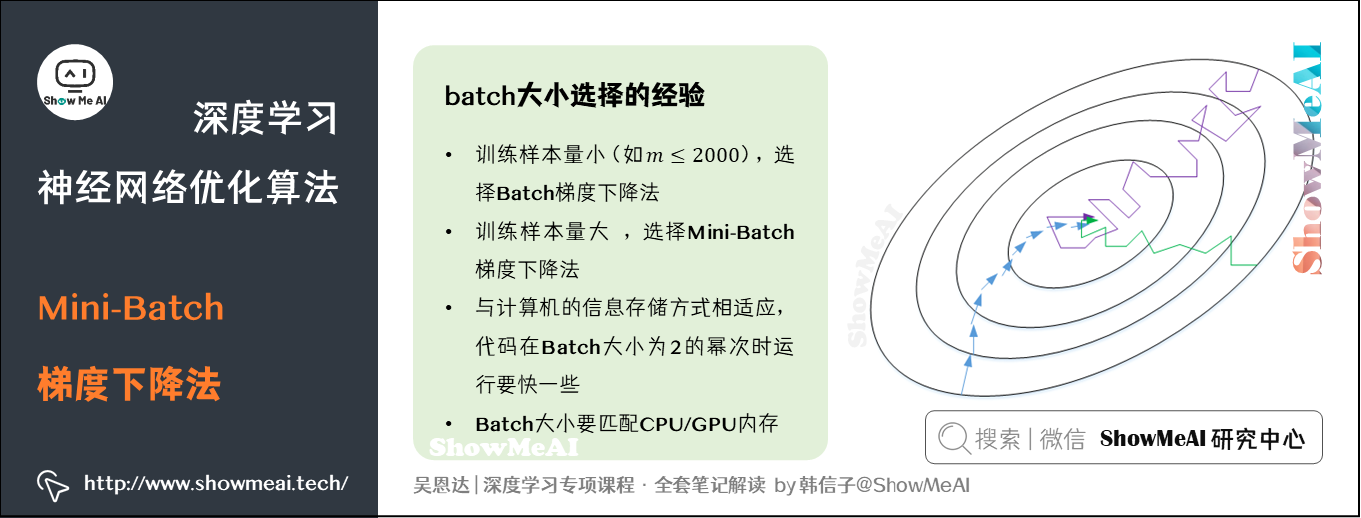
Batch 的大小是重要的超参数，需要根据经验快速尝试，找到能够最有效地减少成本函数的值。

前面提到了 batch 大小的选择方法，当我们确定 batch 大小后，在应用 mini-batch 梯度下降算法时，可以通过以下方式获得 1 个 Batch 的数据：

• 将数据集打乱
• 按照既定的大小分割数据集

其中打乱数据集的代码：

(上述python代码使用到numpy工具库，想了解更多的同学可以查看ShowMeAI 的 图解数据分析 系列中的numpy教程，也可以通过ShowMeAI 制作的 numpy速查手册 快速了解其使用方法)

代码解读：

与 有两处不同：

• 如果传给 一个矩阵，它会返回一个洗牌后的矩阵副本；而 只是对一个矩阵进行洗牌，没有返回值。
• 如果传入一个整数，它会返回一个洗牌后的 。

在进一步讲解优化算法之前，我们来对数学标记做一个统一和说明：

• 我们使用小括号上标 表示训练集里的值， 是第 个训练样本。
• 我们使用中括号上标 表示神经网络的层数， 表示神经网络中第 层的 值。
• 我们使用上标 来代表不同的Batch数据，即 、 。

下面我们将介绍指数加权平均 (Exponentially weighted averages) 的概念。

举个例子，记录半年内伦敦市的气温变化，并在二维平面上绘制出来，如下图所示：

看上去，温度数据似乎有noise，而且抖动较大。如果我们希望看到半年内气温的整体变化趋势，可以通过「移动平均」 (moving average) 的方法来对每天气温进行平滑处理。

例如我们可以设 ，当成第0天的气温值。

第一天的气温与第0天的气温有关：

第二天的气温与第一天的气温有关：

第三天的气温与第二天的气温有关：

即第 天与第 天的气温迭代关系为：

经过「移动平均」 (moving average) 处理得到的气温如下图红色曲线所示：

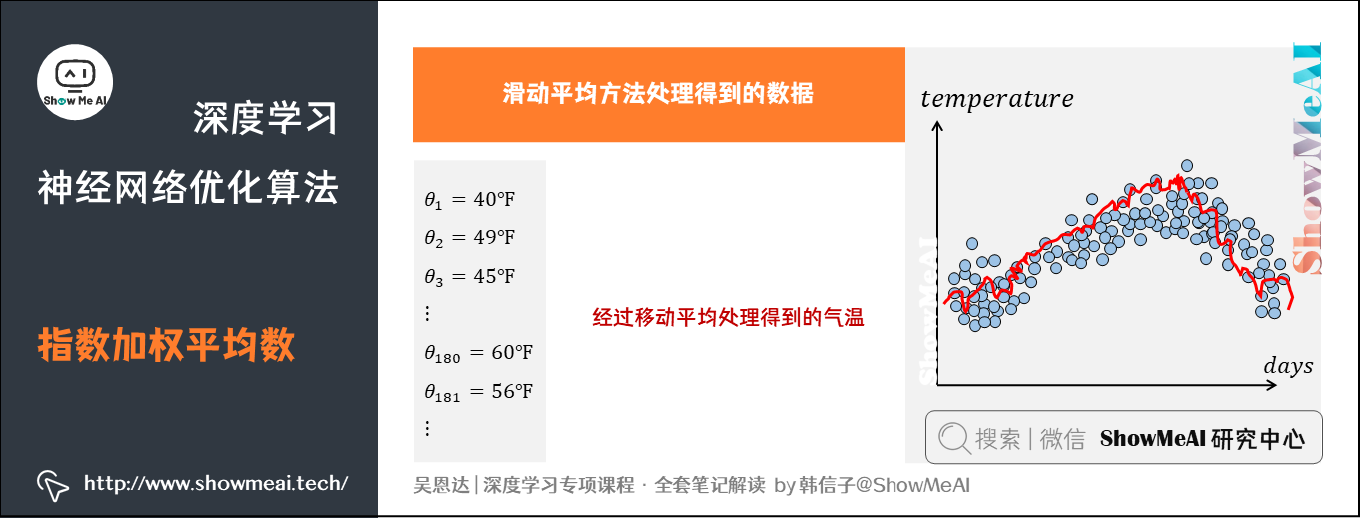
这种滑动平均算法称为指数加权平均 (exponentially weighted average)。根据前面的例子，我们可以看到它的推导公式一般形式为：。

其中指数加权平均的天数由 值决定，近似表示为 。上面的例子中：

• 当 ，则 ，表示将前10天进行指数加权平均。
• 当 ，则 ，表示将前50天进行指数加权平均。

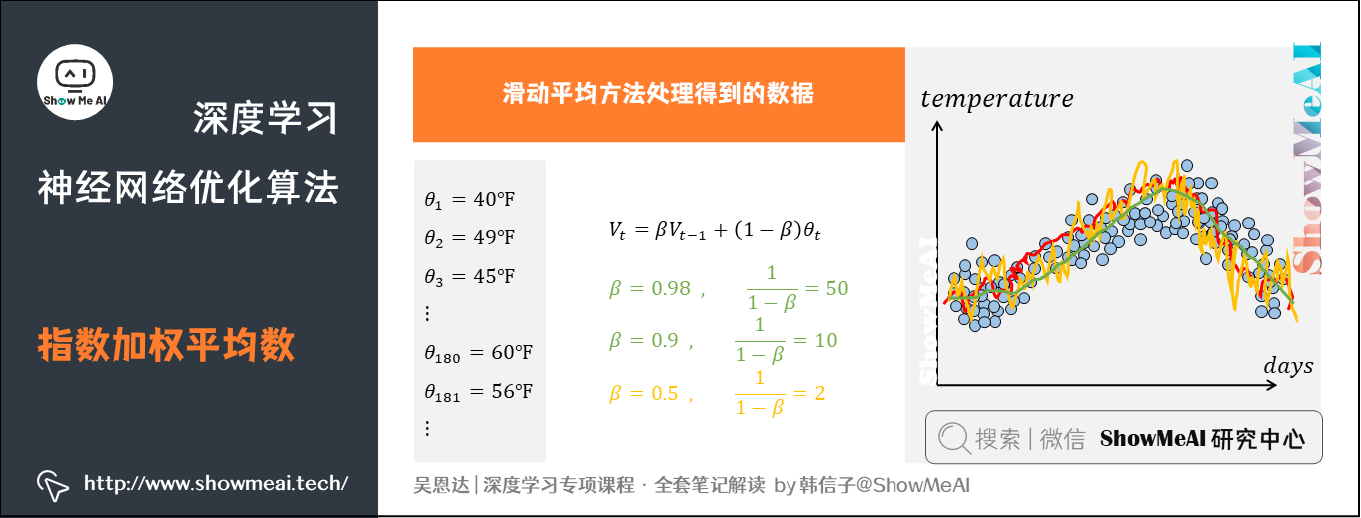
值越大，则指数加权平均的天数越多，平均后的趋势线就越平缓，但是同时也会向右平移。上图中绿色曲线和橙色曲线分别表示了 和 时，指数加权平均的结果。

公式解释：

这里的 是怎么来的呢？就标准数学公式来说，指数加权平均算法跟之前所有天的数值都有关系。

但是指数是衰减的，一般认为衰减到 就可以忽略不计了。因此，根据之前的推导公式，我们只要证明 就好了。

令 ，，则 ，。即证明转化为

显然，当 时，上述等式是近似成立的。这就简单解释了为什么指数加权平均的天数的计算公式为 。

综上，指数加权平均 (Exponentially Weight Average)是一种常用的序列数据处理方式，计算公式为：

其中 为 下的实际值， 为 下加权平均后的值， 为权重值。

指数加权平均数在统计学中被称为“指数加权移动平均值”。

我们将指数加权平均公式的一般形式写下来：

观察上述推导得到的计算公式，其中：

• , , ,..., 是原始数据值。
• , , ,..., 是类似指数曲线，从右向左，呈指数下降的。

如果我们把每个时间点的 和衰减指数写成向量形式，则最终指数加权平均结果 相当于两者的点乘。将原始数据值与衰减指数点乘，相当于做了指数衰减，随距离越远衰减越厉害 (注意到 小于1) ，有如下结论：

• 离得越近的数据点，影响越大，离得越远的数据点，影响越小。

当 时，

展开：

其中， 指第 天的实际数据。所有 前面的系数 (不包括0.1) 相加起来为1或者接近于1，这些系数被称作偏差修正 (Bias Correction)。

根据函数极限的一条定理：

当 时，可以当作把过去10天的气温指数加权平均作为当日的气温，因为10天后权重已经下降到了当天的1/3左右。同理，当 时，可以把过去50天的气温指数加权平均作为当日的气温。

因此，在计算当前时刻的平均值时，只需要前一天的平均值和当前时刻的值。

在实际代码中，只需要不断迭代赋值更新 即可：

指数平均加权并不是最精准的计算平均数的方法，你可以直接计算过去10天或50天的平均值来得到更好的估计，但缺点是保存数据需要占用更多内存，执行更加复杂，计算成本更加高昂。

指数加权平均数公式的好处之一在于它只需要一行代码，且占用极少内存，因此效率极高，且节省成本。

当 时，前面提到的气温示例，指数加权平均结果如绿色曲线。但实际上真实曲线如紫色曲线所示：

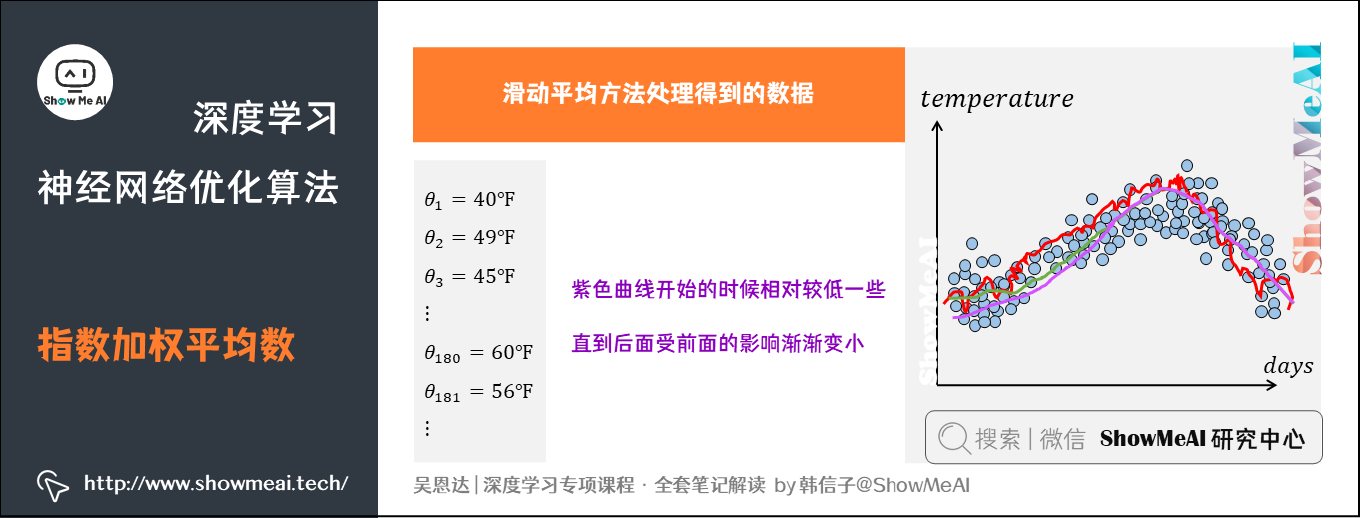
紫色曲线与绿色曲线的区别是，紫色曲线开始的时候相对较低一些。因为开始时设置 ，所以初始值会相对小一些，直到后面受前面的影响渐渐变小，趋于正常。

修正这种问题的方法是进行偏移校正 (bias correction)，即在每次计算完 后，对 进行下式处理：

换算到迭代公式中，即有 。

观察上式：随着 的增大， 的 次方趋近于0。因此当 很大的时候，偏差修正几乎没有作用，但是在前期学习可以帮助更好的预测数据。

大家已经了解了指数加权平均，现在我们回到神经网络优化算法，介绍一下动量梯度下降算法，其速度要比传统的梯度下降算法快很多。做法是在每次训练时，计算梯度的指数加权平均数，并利用该值来更新权重 和常数项 。

具体过程为：

其中，将动量衰减参数 设置为0.9是超参数的一个常见且效果不错的选择。当 被设置为0时，显然就成了 Batch 梯度下降法。

我们用下图来对比一下优化算法的优化过程

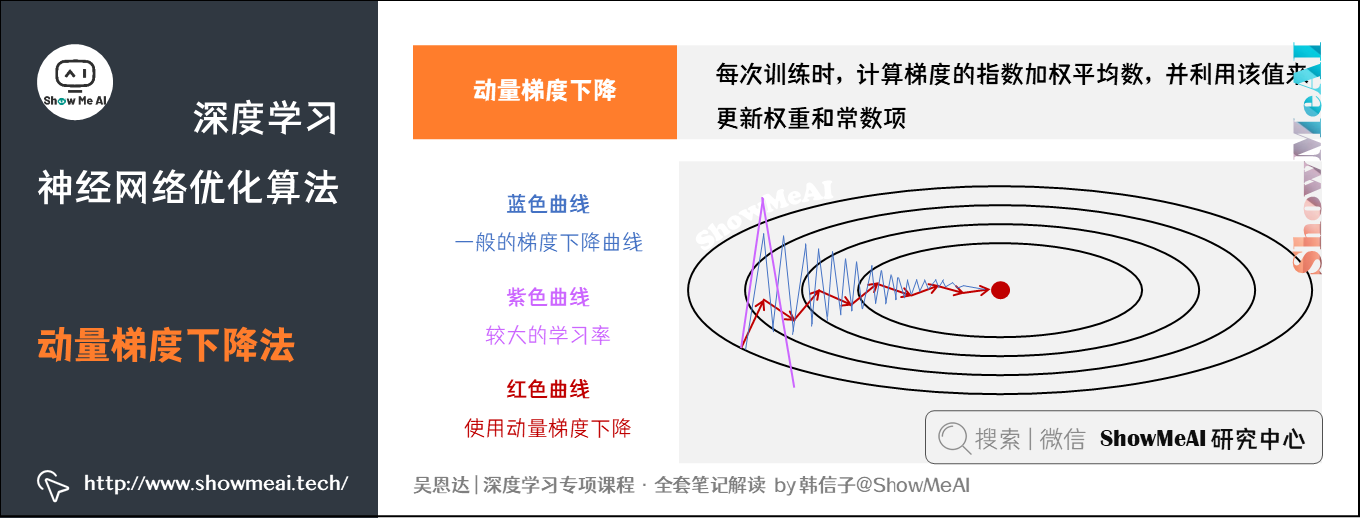
图中：

• 蓝色曲线：使用一般的梯度下降的优化过程，由于存在上下波动，减缓了梯度下降的速度，因此只能使用一个较小的学习率进行迭代。
• 紫色曲线：使用一般梯度下降+较大的学习率，结果可能偏离函数的范围。
• 红色曲线：使用动量梯度下降，通过累加过去的梯度值来减少抵达最小值路径上的波动，加速了收敛，因此在横轴方向下降得更快。

当前后梯度方向一致时，动量梯度下降能够加速学习；而前后梯度方向不一致时，动量梯度下降能够抑制震荡。

另外，在10次迭代之后，移动平均已经不再是一个具有偏差的预测。因此实际在使用梯度下降法或者动量梯度下降法时，不会同时进行偏差修正。

补充：在其它文献资料中，动量梯度下降还有另外一种写法：

即消去了 和 前的系数 。这样简化了表达式，但是学习因子 相当于变成了 ，表示 也受 的影响。从效果上来说，这种写法也是可以的，但是不够直观，且调参涉及到 ，不够方便。所以，实际应用中，推荐第一种动量梯度下降的表达式。

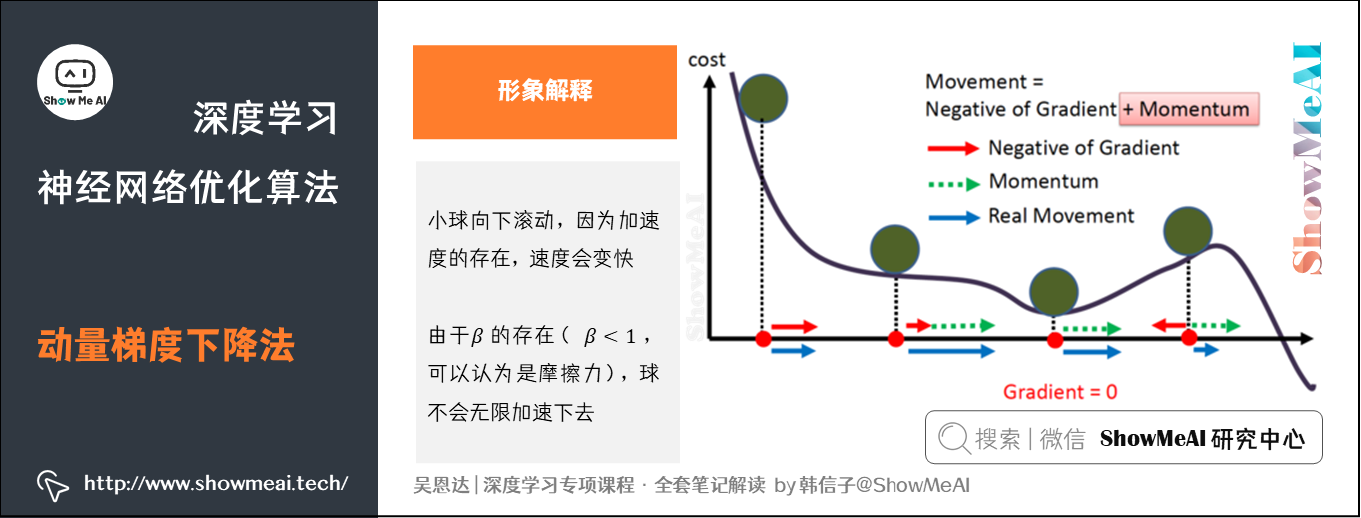
将成本函数想象为一个碗状，从顶部开始运动的小球向下滚，其中 ， 想象成球的加速度；而 、 相当于速度。

小球在向下滚动的过程中，因为加速度的存在速度会变快，但是由于 的存在，其值小于1，可以认为是摩擦力，所以球不会无限加速下去。

RMSProp (Root Mean Square Propagation，均方根传播) 是另外一种优化梯度下降速度的算法，它在对梯度进行指数加权平均的基础上，引入平方和平方根。具体过程为 (省略了 ) ：

其中， 是一个实际操作时加上的较小数 (例如 ) ，为了防止分母太小而导致的数值不稳定。

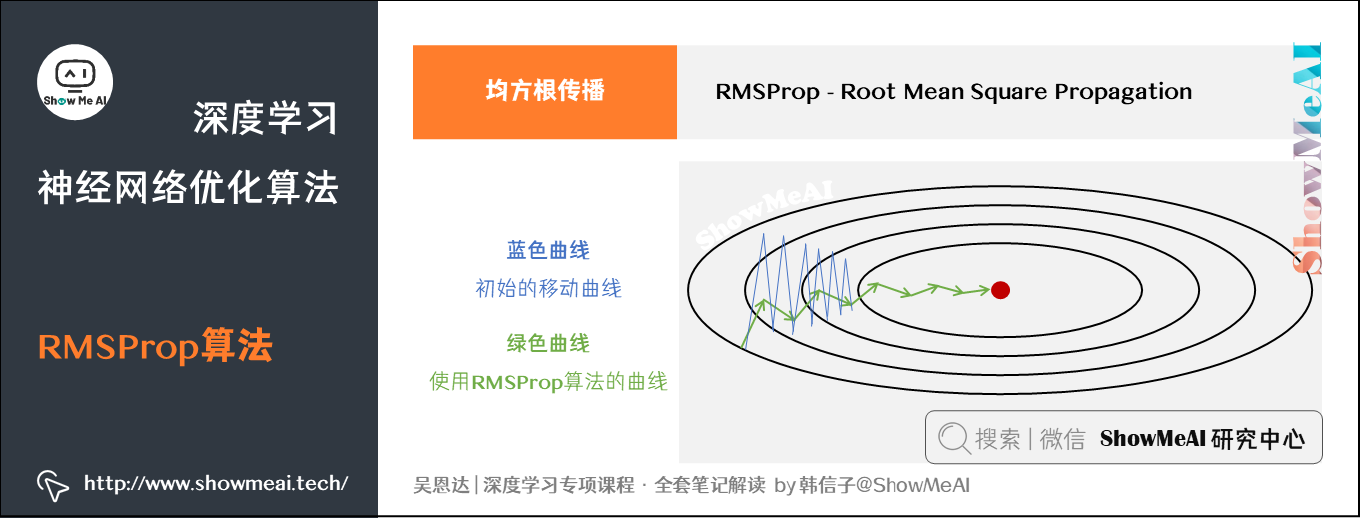
如图所示，蓝色轨迹代表初始的移动，可以看到在 方向上走得比较陡峭 (即 较大) ，相比起来 较小，这影响了优化速度。

因此，在采用RMSProp算法后，由于 较小、 较大，进而 也会较小、 也会较大，最终使得 较大，而 较小。后面的更新就会像绿色轨迹一样，明显好于蓝色的更新曲线。RMSProp减小某些维度梯度更新波动较大的情况，使下降速度变得更快。

RMSProp有助于减少抵达最小值路径上的摆动，并允许使用一个更大的学习率 ，从而加快算法学习速度。并且，它和Adam优化算法已被证明适用于不同的深度学习网络结构。

注意， 也是一个超参数。

对比原始梯度下降与RMSProp算法优化过程，如下图所示 (上方为原始梯度下降，下方为RMSProp)

Adam (Adaptive Moment Estimation，自适应矩估计)算法结合了动量梯度下降算法和RMSprop算法，通常有超越二者单独时的效果。具体过程如下 (省略了 ) ：

首先进行初始化：

用每一个Mini-Batch计算 、 ，第 次迭代时：

一般使用Adam算法时需要计算偏差修正：

所以，更新 、 时有：

Adam优化算法有很多的超参数，其中

• 学习率 ：需要尝试一系列的值，来寻找比较合适的
• ：常用的缺省值为0.9
• ：Adam算法的作者建议为0.999
• ：不重要，不会影响算法表现，Adam算法的作者建议为

  、 、 通常不需要调试。

对比原始梯度下降与RMSProp算法优化过程，如下图所示 (上方为原始梯度下降，下方为Adam)

减小学习率 也能有效提高神经网络训练速度，这种方法被称为学习率衰减法 (learning rate decay)。

学习率衰减就是随着迭代次数增加，学习率 逐渐减小。如下图示例。

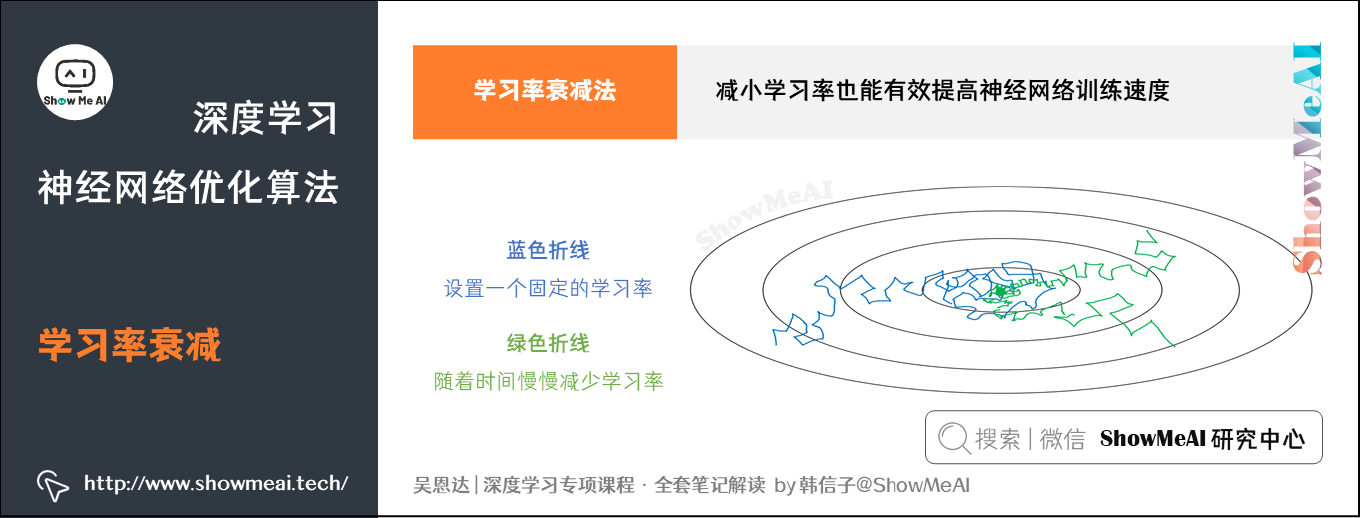
① 蓝色折线表示设置一个固定的学习率

• 在最小值点附近，由于不同的Batch中存在一定的噪声，因此不会精确收敛，而是始终在最小值周围一个较大的范围内波动。

② 绿色折线表示随着时间慢慢减少学习率 的大小

• 在初期 较大时，下降的步长较大，能以较快的速度进行梯度下降；
• 后期逐步减小 的值，即减小步长，有助于算法的收敛，更容易接近最优解。

最常用的学习率衰减方法：

其中，decay_rate为衰减率 (超参数) ，epoch_num为将所有的训练样本完整过一遍的次数。

• 指数衰减：
• 其他：
• 离散下降

对于较小的模型，也有人会在训练时根据进度手动调小学习率。

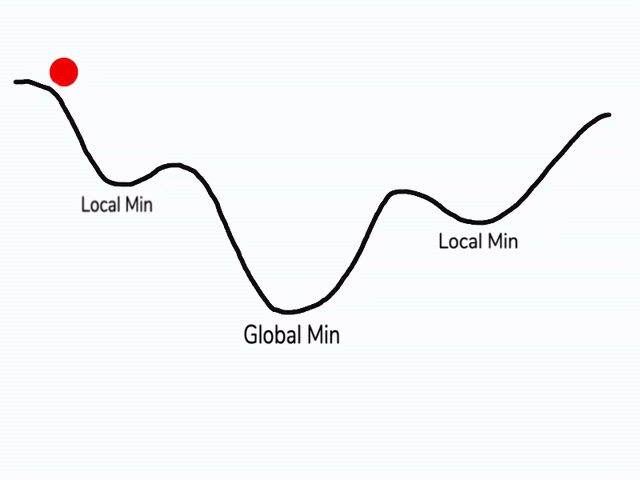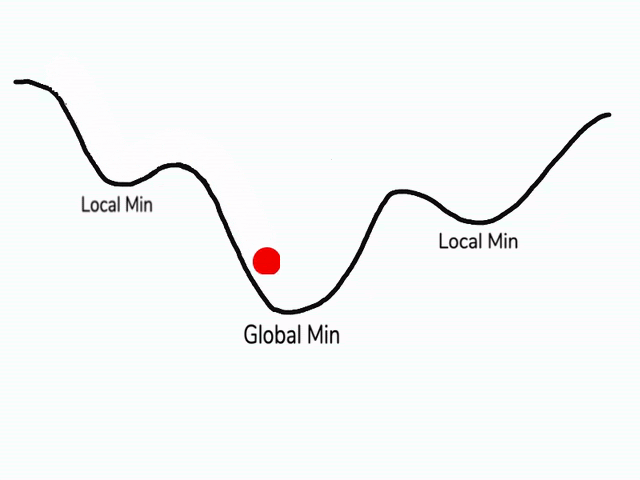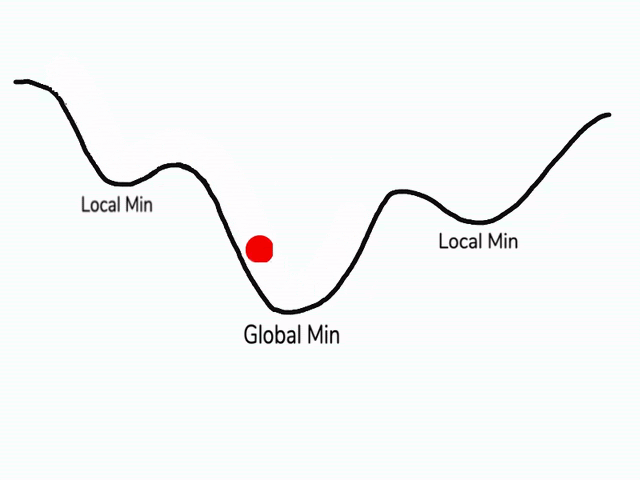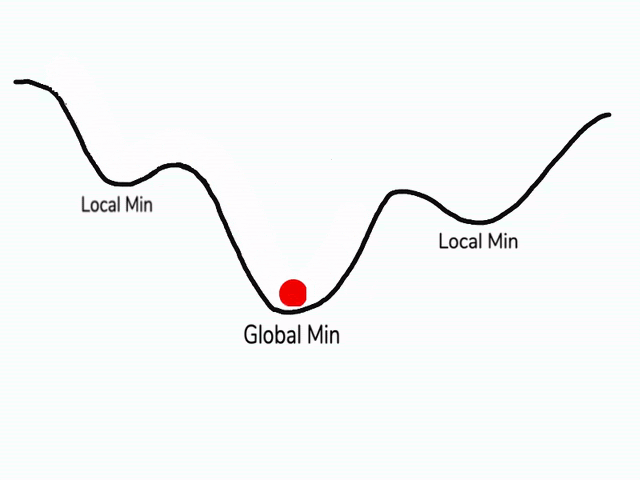
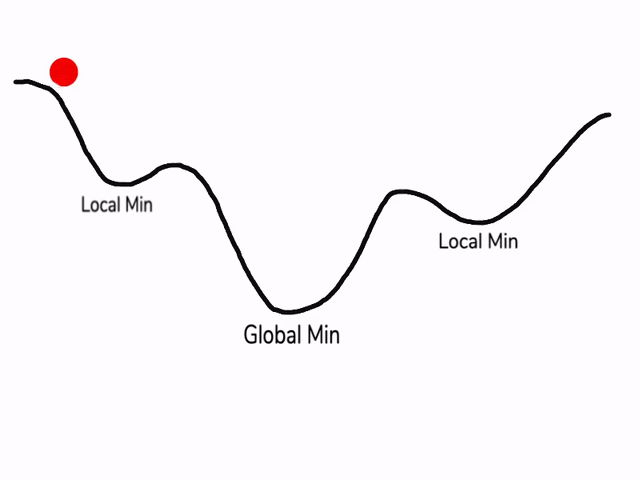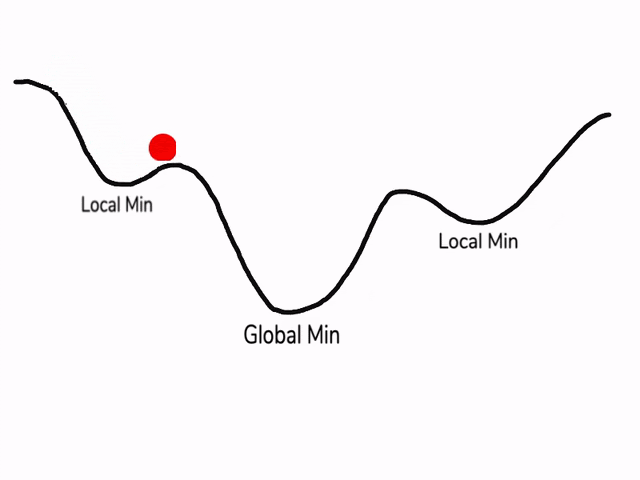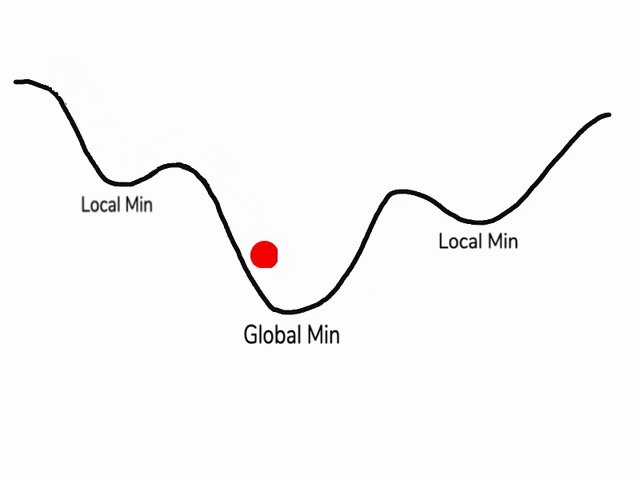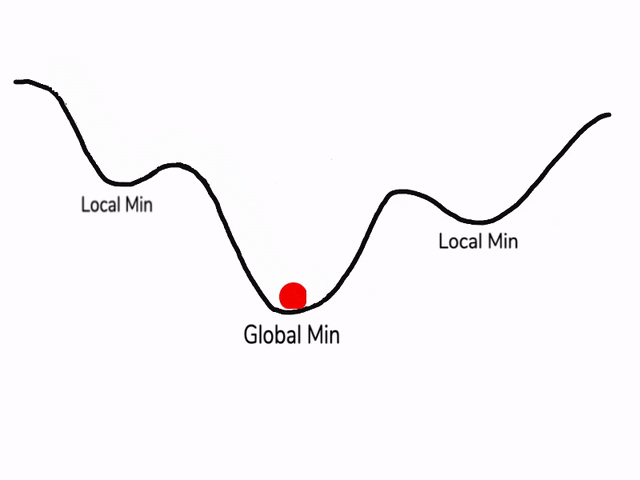
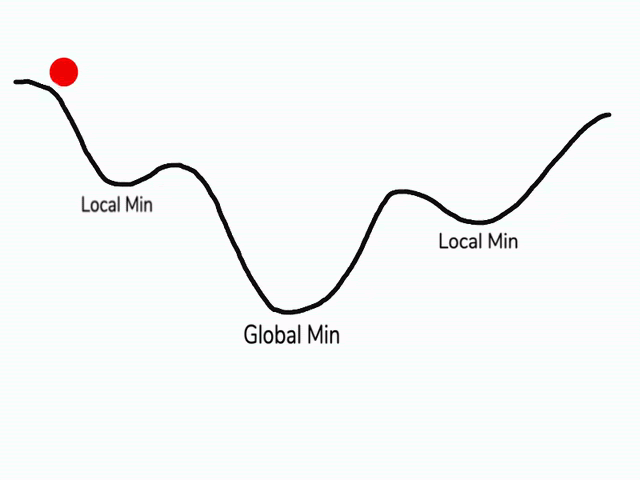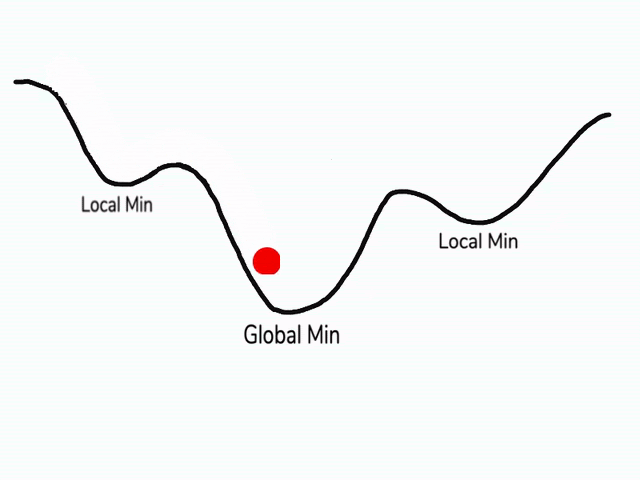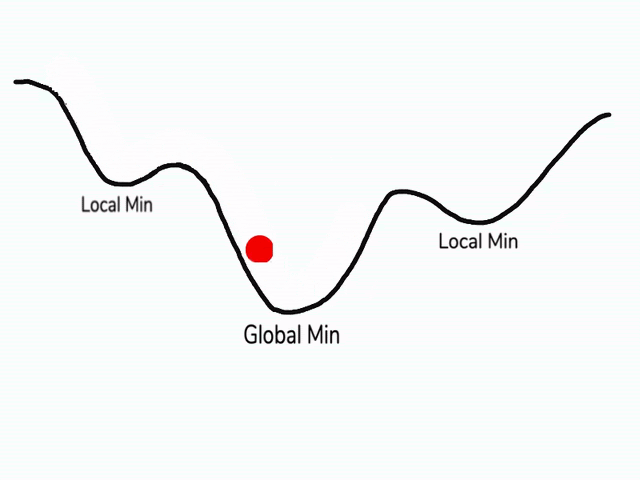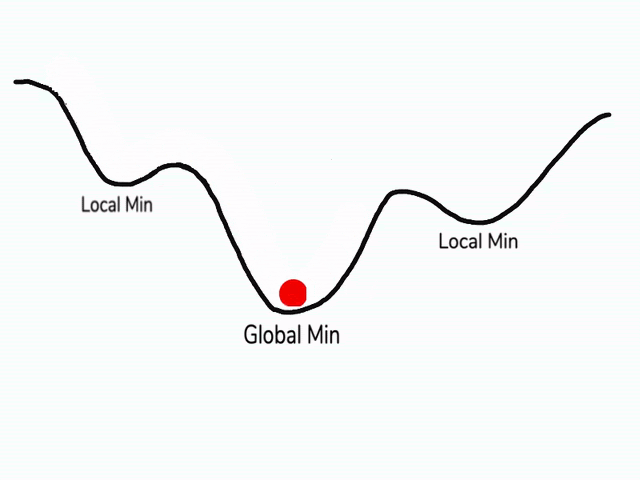
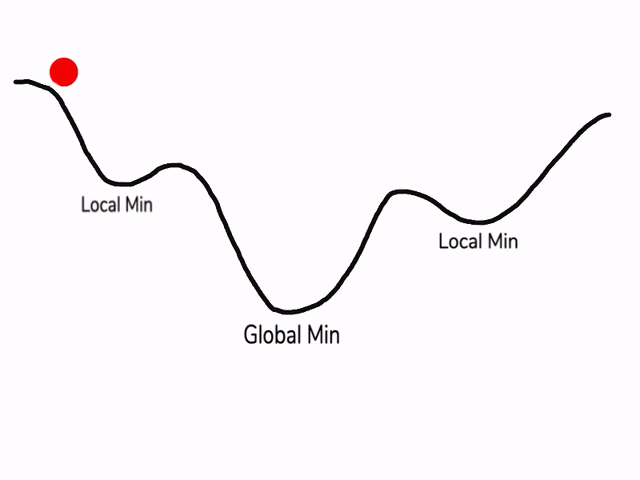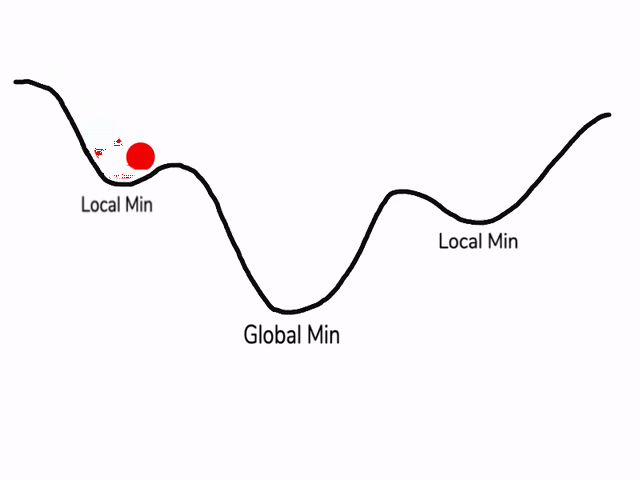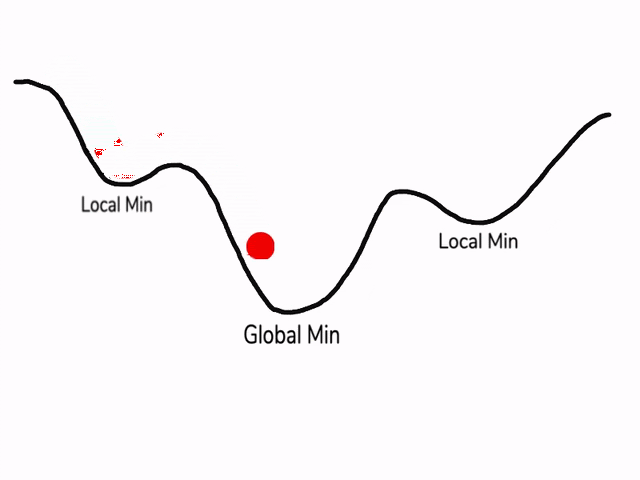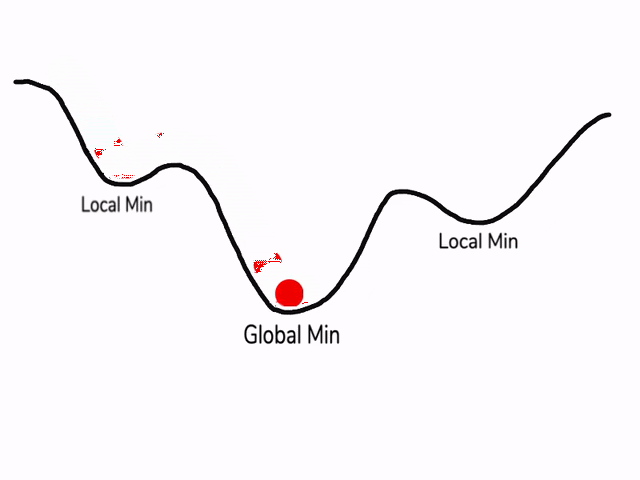
在使用梯度下降算法不断减小cost function时，可能会得到局部最优解 (local optima)而不是全局最优解 (global optima)。

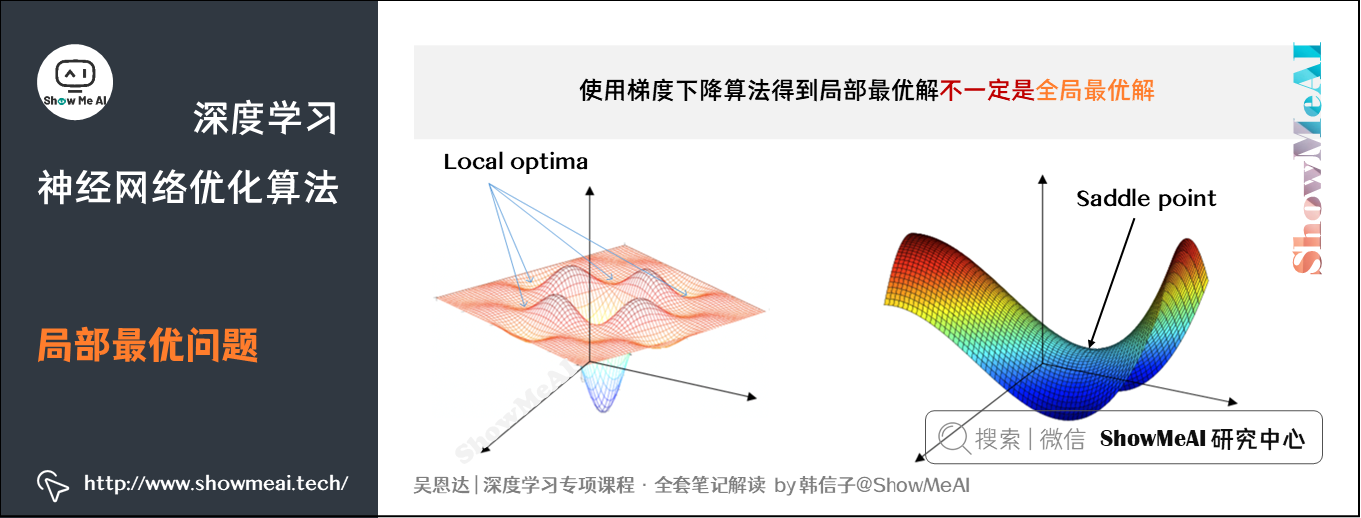
之前我们对局部最优解的理解是形如碗状的凹槽，如图左边所示。但是在神经网络中，local optima 的概念发生了变化。准确来说，大部分梯度为零的“最优点”并不是这些凹槽处，而是形如右边所示的马鞍状，称为 saddle point。

所以在深度学习损失函数中，梯度为零并不能保证都是 convex (极小值)，也有可能是 concave (极大值)。特别是在神经网络中参数很多的情况下，所有参数梯度为零的点很可能都是右边所示的马鞍状的 saddle point，而不是左边那样的 local optimum。

类似马鞍状的 plateaus 会降低神经网络学习速度。Plateaus 是梯度接近于零的平缓区域，如图所示。在 plateaus 上梯度很小，前进缓慢，到达 saddle point 需要很长时间。到达 saddle point 后，由于随机扰动，梯度一般能够沿着图中绿色箭头，离开 saddle point，继续前进，只是在 plateaus 上花费了太多时间。

结论：

• 在训练较大的神经网络、存在大量参数，并且成本函数被定义在较高的维度空间时，困在极差的局部最优中是不大可能的；
• 鞍点附近的平稳段会使得学习非常缓慢，而这也是动量梯度下降法、RMSProp 以及 Adam 优化算法能够加速学习的原因，它们能帮助尽早走出平稳段。

• 图解数据分析
• numpy速查手册

• 大厂技术实现 | 推荐与广告计算解决方案
• 大厂技术实现 | 计算机视觉解决方案
• 大厂技术实现 | 自然语言处理行业解决方案
• 图解Python编程：从入门到精通系列教程
• 图解数据分析：从入门到精通系列教程
• 图解AI数学基础：从入门到精通系列教程
• 图解大数据技术：从入门到精通系列教程
• 图解机器学习算法：从入门到精通系列教程
• 机器学习实战：手把手教你玩转机器学习系列
• 深度学习教程 | 吴恩达专项课程 · 全套笔记解读
• 自然语言处理教程 | 斯坦福CS224n课程 · 课程带学与全套笔记解读

• 深度学习教程 | 深度学习概论
• 深度学习教程 | 神经网络基础
• 深度学习教程 | 浅层神经网络
• 深度学习教程 | 深层神经网络
• 深度学习教程 | 深度学习的实用层面
• 深度学习教程 | 神经网络优化算法
• 深度学习教程 | 网络优化：超参数调优、正则化、批归一化和程序框架
• 深度学习教程 | AI应用实践策略 (上)
• 深度学习教程 | AI应用实践策略 (下)
• 深度学习教程 | 卷积神经网络解读
• 深度学习教程 | 经典CNN网络实例详解
• 深度学习教程 | CNN应用：目标检测
• 深度学习教程 | CNN应用：人脸识别和神经风格转换
• 深度学习教程 | 序列模型与RNN网络
• 深度学习教程 | 自然语言处理与词嵌入
• 深度学习教程 | Seq2seq序列模型和注意力机制