动态最优化基础——学习笔记01_耀世娱乐-耀世平台珠宝有限公司

动态最优化基础——学习笔记01

栏目：耀世平台发布时间：2024-05-26 09:09:50

在中级微观经济学中，我们常常使用拉格朗日乘数法等方法求解某个问题的最优解，但我们所得到的结果往往只是某个选择变量的单个最优值，计算得到的结果只能支持我们进行一次决策。这种方法在解决静态优化问题时通常是有效的。当我学习到增长理论时，我们就会开始考虑一个时间路径上的选择。比如某消费者A拥有预算Y，效用和货币的折现率不同，那么在一定时期T中，A该如何花掉他手上的这笔钱来得到最大的效用呢？

在这种情况下，我们曾经无往而不利的方法就难以继续解决问题了，因为现在面临的是一个动态的问题，我们被要求在给定条件下，求得一个最优路径（在这个问题里就是每一个时点上A应该花掉的货币数量），曾经针对某个时点求取当前最优值的方法有的不能用了，有的用来求解过于麻烦。在这种情况下，我们就应该拓展我们的数学工具，来学习动态最优化。

我学习动态最优化的教材是蒋中一的《动态最优化基础》，把学习笔记放在这里供大家参考。

1.动态最优化问题：在整个计划期内的每个时期(离散时间情形)或给定时间区间如[0,T]中的每个时刻，选择变量的最优值是什么？

也就是说，我们要对每个时期或时刻的选择变量都确定一个值，使得这样选择的结果能使我们得到我们想要的结果(比如最大化、最小化某个函数)。当我们确定下来之后，这些值以及对应的时间就构成了一条最优时间路径。其中，我们用符号 * 代表最优，时间路径用 $y(t)$ 表示，连续时间下的某个变量y的最优时间路径用 $y^*(t)$ 表示。

学习过博弈论的朋友都知道，在每时每刻作出当前阶段最优的选择并不代表着结果是最优的，这里也是一样：每时每刻最优不代表最优路径。因为我们想要的最优是从上帝视角看在整个计划期内的整体是最优的。

2.两类情形

通常我们把问题分为两类：离散情形、连续变量情形

离散情形如下图，我们从A点前往Z点，每条路上标的值为过路费，如何选择使过路费最小？

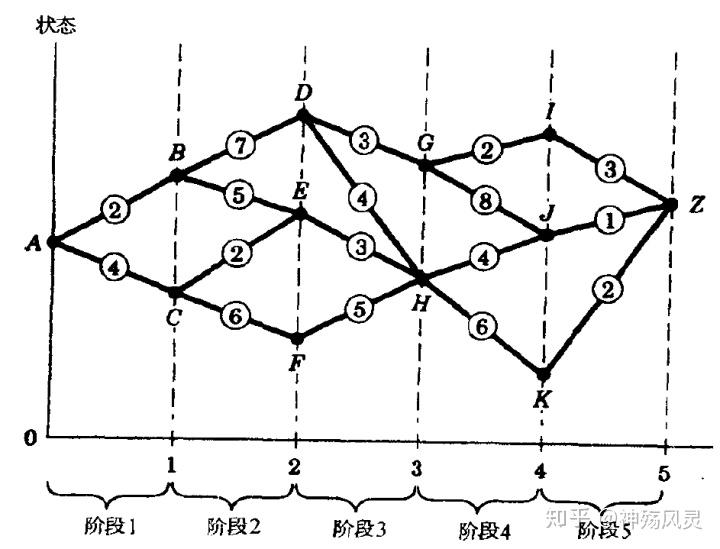
连续变量情况如下图，同样从A点到Z点，如何选择使得路径最短？

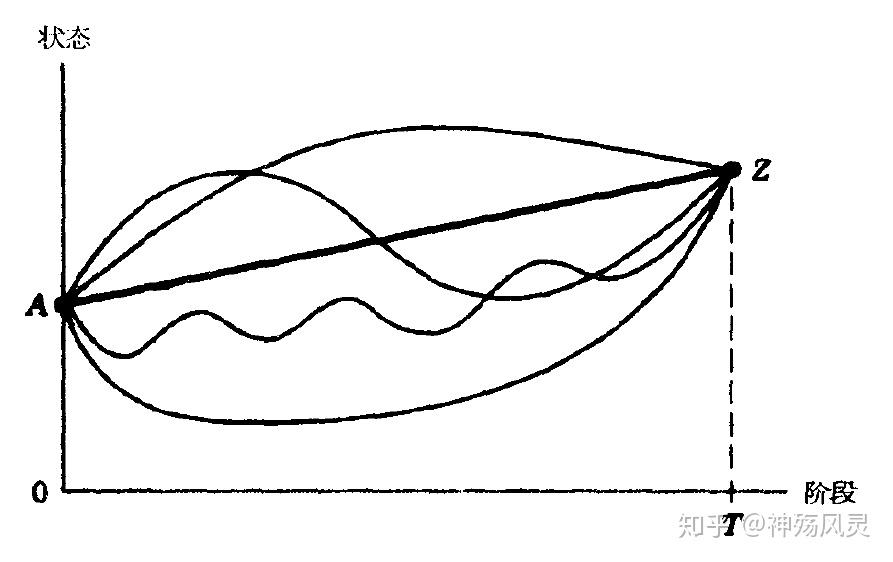
3.基本要素

简单的动态最优化问题有四个基本要素：

给定初始点和终结点
从初始点到终结点的至少一组可行路径
充当路径表现指标的一组路径值
特定的目标

路径表现指标就是说我们用什么方法对路径进行排序，然后用一个指标(一般就是实数)表示这个排序。

特定的目标就是我们想要得到什么，最短的路径？最长的路径？总效用最大？还是什么？

4.泛函

泛函就是从路径(曲线)到实数(表现指标)的映射。

$泛函：路径(曲线)\\rightarrow实数(表现指标)$
这里的实数我们用 $V$ 表示，路径用 $y(t)$ 表示，因此将映射或泛函记为 $V[y(t)]$ 。

注意： $V[y(t)]$ 不代表 $V$ 是 $t$ 的函数，因为成分 $y(t)$ 是一个整体，代表着一条时间路径，即 $V[y(t)]$ 仅是 $y(t)$ 的函数，甚至一般为了避免误会，将其记为 $V[y]$ 。

5.几个记号

$O$ ：初始时间
$T$ ：终结时间
$A$ ：初始状态
$Z$ ：终结状态

6.问题的分类

根据终结时间的不同，将动态最优化问题分为：有限计划跨度( $T$ )和无限计划跨度( $\\infty$ )。

可变终结点：

固定时间问题（T固定，Z自由）——垂直终结线问题
固定端点问题（T自由，Z固定）——水平终结线问题
终结曲线（曲面）问题—— $Z=\\phi(T)$

可变初始点：初始状态不受约束

这里因为初始时间无论是多少我们都可以设为 $O$ ，因此不存在初始时间不固定的问题，也不存在初始为曲线、曲面的问题。

三个图例：

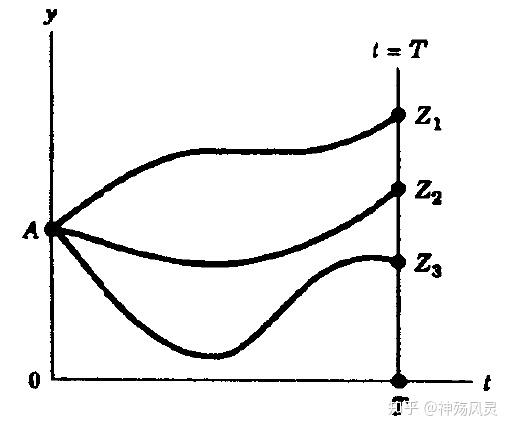
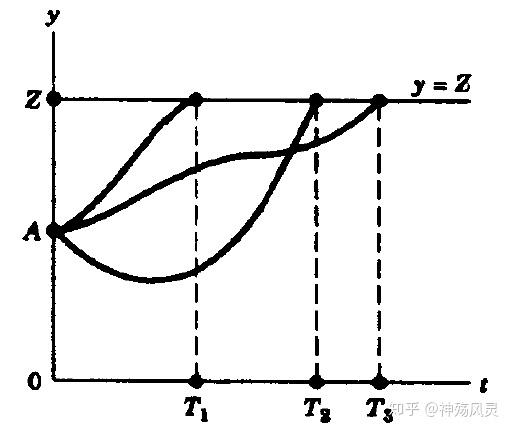
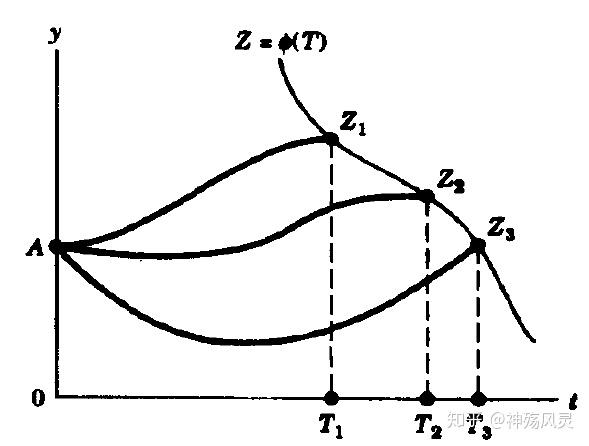
7.横截条件

当我们求出某个可能的最优路径时，我们求得的通常不是一条确定的路径，而是多组路径或者一系列路径，此时就需要我们用限制条件来从所以可能路径中筛选出最优路径。其中我们要注意到，可变终结点问题相比固定终结点问题多一个自由度，相应的我们就需要一个额外的条件。我们的最优路径一定是穿过我们所给的限制条件的，因此我们称这种条件为横截条件（横截是穿过的意思），也称 $TVC$ 条件。

8.如何表示泛函

在离散问题中，路径值是每一段弧线的值的总和，也就是： $路径值=\\sum成分弧值$

在连续问题中，类似的有 $V[y]=\\int_{0}^{T}(弧值)dt$ ，那么问题来了，我们怎么表示这个弧值呢？

我们对每一段无限小的弧，想要识别它，需要从几方面入手：

开始时间—— $t$
开始状态—— $y(t)$
弧的前进方向—— $y'(t)=\\frac{dy}{dt}$

根据这些信息，我们就能分辨出每个微小的弧，但这还不够，我们之前说了要有一个表现指标，也就是将每个路径对应到一个表现指标上，那么分解到每个弧，我们要给它一个值，因此我们使用一个弧值指派函数： $F[t,y(t),y'(t)]$

通常我们可以把路径值泛函（弧值之和）写作定积分形式：

即泛函的定积分形式： $V[y]=\\int_{0}^{T}F[t,y(t),y'(t)]dt$

当然，如果我们拥有两个状态变量 $y,z$ ，则我们同时需要考虑 $y$ 和 $z$ 上的弧值，则我们的目标泛函就表示为 $V[y,z]=\\int_{0}^{T}F[t,y(t),y'(t),z(t),z'(t)]dt$

9.其他形式的泛函

当最优化值不依赖路径的中间位置，只依赖于终结点位置时，由于没必要加总弧值，此时记目标泛函为 $V[y]=G[T,y(T)]$ ,G仅仅依赖于终结时点下所发生的情况。（迈耶问题）
当状态变量增多时，我们有 $V[y,z]=G[T,y(T),z(T)]$

当两种情况同时发生的时候，我们有 $V[y]=\\int_{0}^{T}F[t,y(t),y'(t)]dt+G[T,y(t)]$ （博尔扎问题）

10.几种情况的转化

标准问题： $V[y]=\\int_{0}^{T}F[t,y(t),y'(t)]dt$
迈耶问题： $V[y]=G[T,y(T)]$
博尔扎问题： $V[y]=\\int_{0}^{T}F[t,y(t),y'(t)]dt+G[T,y(t)]$

迈耶问题 $\\rightarrow$ 标准问题

定义 $z(t)\\equiv G[t,y(t)]$ ,满足初始条件 $z(0)=0$ ,
此时有 $\\int_0^T z'(t)dt=z(t)|_0^T=z(T)=G[T,y(T)]$ ,
将 $z'(t)$ 看作 $F[t,y(t),y'(t)]$ 的特殊情形，这就完成了从迈耶问题向标准问题的转化，
有 $V[y]=\\int_0^T z'(t)dt$

博尔扎问题 $\\rightarrow$ 标准问题

设 $z(t)=G[t,y(t)]$ ,满足 $Z(0)=0$ ,
有 $V[y]=\\int_0^T F[t,y(t),y'(t)]dt + \\int_0^T z'(t)dt=\\int_0^TH[t,y(t),y'(t)]dt$
博尔扎问题 $\\rightarrow$ 迈耶问题

设 $z'(t)=F[t,y(t),y'(t)]$ ,满足 $z(0)=0$ ,
有 $V[y]=\\int_0^T z'(t)dt +G[T,y(t)]=z(T)+G[T,y(t)]=H[T,y(t)]$

11.动态最优化问题的几种处理方法

变分法

变分法的最基本问题是关于单个状态变量，且具有给定初始点和终结点，没有额外约束

$\\begin{align}max(min) \\qquad V[y]&=\\int_0^T F[t,y(t),y'(T)]dt \\\\ s.t \\qquad \\qquad y(0)&=A \\\\ y(T)&=Z \\end{align}$

当然在这里我们假设泛函是可积的，即积分必须收敛，更进一步假设问题中所有函数是连续的和连续可微的。

最优控制理论

在最优控制理论中，我们认为动态最优化问题由三个类型的变量构成：时间变量 $t$ ，状态变量 $y(t)$ 和控制变量 $u(t)$ 。因此，我们的关注点转移到了控制变量上。此时，为了我们在得到 $u(t)$ 后能够获得问题的解，我们必须在给定关于 $y$ 的初始条件后能够通过 $u(t)$ 得到 $y(t)$ 。因此我们需要一个额外的方程将二者联系起来，这就是运动方程（状态方程）。

一般把方程写为 $\\frac{dy}{dt}=f[t,y(t),u(t)]$ ,这样我们就可以通过最优控制变量路径得到相关的状态变量路径。对应于变分法，我们把问题写为：

$\\begin{align}max(min) \\qquad V[u]&=\\int_0^T F[t,y(t),u(t)]dt \\\\ s.t \\qquad \\qquad y'(t)&=f[t,y(t),u(t)]\\\\ y(0)&=A \\\\ y(T)&=Z \\end{align}$